Nonograms

Nonograms are tricky logic puzzles that reward you with a solution picture at the end. Color in some cells and mark others as free — step by step you get closer to the goal.

Rules for black-and-white Nonograms

• Every number stands for the length of a cell block (group of black cells).
• The order of the numbers correlates exactly with the actual order of blocks.
• While the length and order of blocks is known, their exact position is not.
• There must be at least one free cell between two black blocks.

Rules for color Nonograms

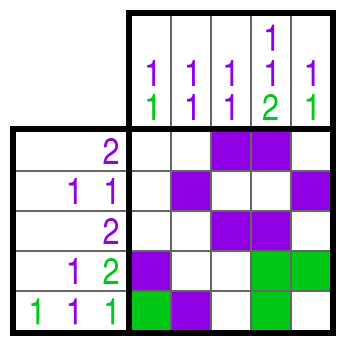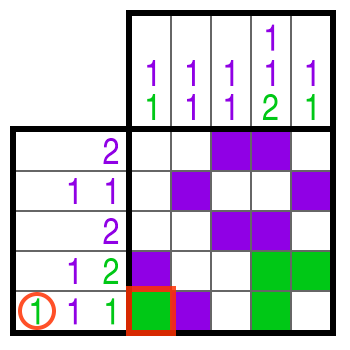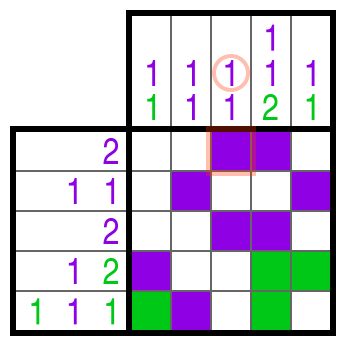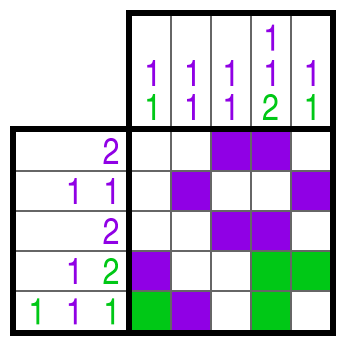
In principle, color Nonograms have the same rules as black-and-white Nonograms. However, there are two things that are to be taken into account:

• The color of each number hint determines the color of each cell block.
• Blocks of different colors can touch. (Free cells between blocks of different colors are not required.)

Example for a black-and-white Nonogram

In the following, we show you step by step how to solve a small black-and-white Nonogram. Of course, normal Nonograms are larger and result in a real picture.

Step 1

Let’s start with row 2: There are a total of 3 possibilities to place both blocks. You can see that in each case the second cell of the row is black. Thus, we paint the cell with black.
Note:
In chapter "Solution techniques" (keyword: slide technique) we explain how to make such steps with large Nonograms.

Step 2

Let’s continue with the very last row. There, a block of three black squares is to be placed. In this row, too, there are only 3 possibilities. In each of the 3 possible cases, the third cell of the row is black. So, we color it in with black.

Step 3

In column 3, we know the exact position of the block of 3 squares. We fill it in entirely and can cross out the number hint "3".
Since no other block is to be placed in the column, we can mark the two remaining cells as free (with a small dot).
Note:
As a general rule — whenever you know that a cell must remain free, mark this cell with a dot!

Step 4

Step 5

Step 6

Step 7

Step 8

The Nonogram is solved!

Chapter "Solution techniques" gives you deeper insight into solving both black-and-white and color Nonograms.

Even if you know the Nonogram rules, every beginning is difficult. Here we show you the most important techniques to solve Nonograms successfully.

Slide technique (1)

(a)

We don't know where exactly the block of 7 squares should be in figure (a), but there are some cells that must be black in any case. How to find them? Place the block in your mind (or with the aid of counting arrows, see below) as far to the left as possible and as far to the right as possible. Those cells where both extreme cases overlap, certainly belong to the block and must be painted black. If you play Nonograms on paper, you usually count cells starting from both sides and make light marks with your pencil. The counting mode with its blue counting arrows enables you to do the same in our app on the screen!

(b)

However, if there is no overlap as seen with the block of 4 squares in figure (b), no cells can be colored in.

Slide technique (2)

(c)

Of course, the slide technique can be also applied if there is more than one block in the row or column in question, see figure (c). Again, place the blocks in your mind (or with the aid of counting arrows) as far to the left as possible. Always remember that there has to be one free cell at least between two blocks of the same color. Then place the blocks as far to the right as possible. Paint those cells where the same block overlaps.

Slide technique (3)

(d)

If some cells are already determined, as seen in figure (d), these cells can be additionally taken into account when sliding the blocks in your mind. That way you can possibly achieve even more overlaps. That means for our example: The block of 2 squares cannot be placed further to the left because of the existing cell marked as free. In the opposite direction, the block of 4 squares cannot be positioned further to the right than shown. Thus, there is more overlap than in the previous example.

Slide technique (4)

(e)

Since with color Nonograms there don't have to be free cells between blocks of different color, counting arrows belonging to different colors are placed together without gap generally (this is shown in example (e) when counting from the left to the right).
However, with color Nonograms additional information can be gained: If a row is being considered, the number hints of the columns (and also the determined cells in the columns) can provide important information. (Similarly, if a column is being considered, you can gain information from the rows.)
In our example, there should be only one black block of 7 squares in column 6. This means the red block of 4 squares of the considered row cannot hit column 6. Thus, the extreme positioning of the block of 4 squares is situated three cells further to the left than without this additional information.

Further examples

Example (f)

(f)

Example (g)

(g)

Example (h)

(h)

Example (i)

(i)

Example (j)

(j)

Techniques for color Nonograms

In figure (e), color Nonograms have already been addressed. Here, three further examples specific to color Nonograms are shown.

(k)

In row 1, a single black square is to be positioned. Since in columns 4 and 5 only red blocks are intended, the intersections must be free. Though for column 2 a black block of 2 squares is demanded, there should be a red square above. Thus, the cell in row 1 / column 2 must be free.

(l)

In all rows – except for row 2 – a black block is required first. Thus, the red single square of column 1 can only be placed in row 2.

(m)

In column 3, the red block has already been placed. This means, only the black block is missing. This is why the third cell of row 2 cannot be red and thus must be free.

Besides the techniques presented on this page, there are a lot of other techniques, of course. Certainly, you will find them by yourself in the course of time. Have fun!