Campixu

Numbers

• Each row and each column holds exactly two numbers.
• The first number indicates how many cells in the corresponding row or column are black (independently of their grouping).
• The second number indicates the number of black blocks (groups) in the row or column. A block is a sequence of (at least 1) black cells. Between two blocks, there is always at least 1 empty cell to separate them.
• Thus, [5 3] reads: “5 black cells are grouped in 3 blocks.” This can be 1+1+3 or 1+3+1 or 3+1+1 or 1+2+2 or 2+1+2 or 2+2+1. The exact position and order of the blocks is not specified.

Bordered regions

• All cells within a bordered region must have the same color. Either all cells are black or all cells are empty.
• This means, if you know the color of one cell, you can mark the other cells of the bordered region in the same way, black or empty. (Flooding a region)

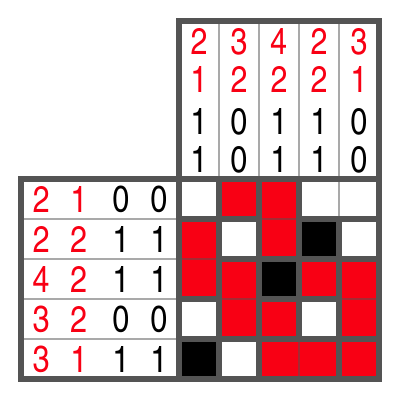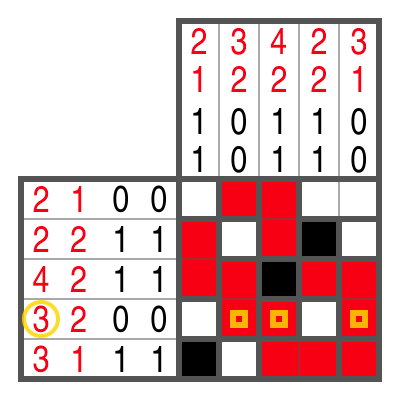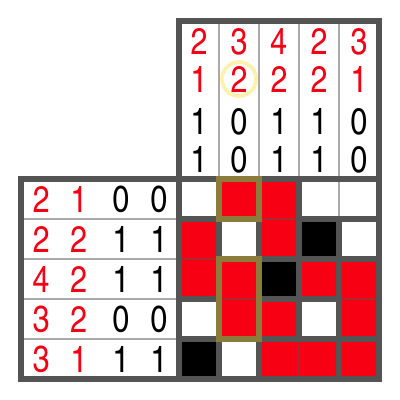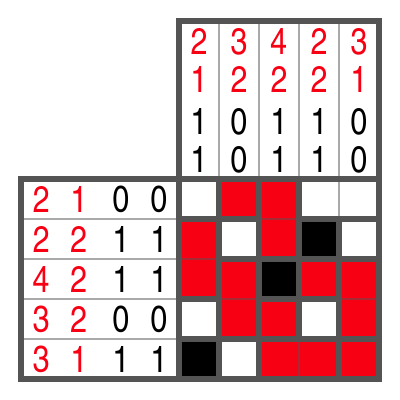
Color Campixu works in principle in the same way as the black-and-white version. But there are three things to consider:

• For each color, there are two numbers in each row and column that indicate how many cells and blocks of that color exist.
• There does not necessarily have to be a free cell between two blocks of different colors.
• The order of colors is never specified.

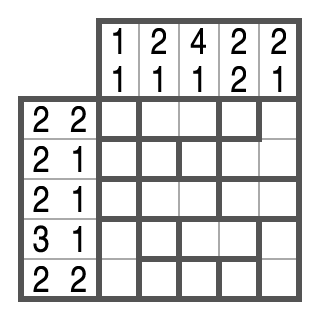
Example of a black-and-white Campixu

In the following, we will show you step by step how to solve a small black-and-white Campixu. Normal Campixu puzzles are larger, of course.

Step 1

In row 1, 2 black cells are to be placed in 2 blocks. This means that each block must be exactly 1 cell wide. Because the 2nd and 3rd cell belong to the same region, they would form a block of 2 if they were colored black. Therefore, they must be marked as free.
Note:
In general: Whenever you know that cells must remain empty, mark these cells with a dot!

Step 2

In row 3, there should be exactly one block of 2. The first cell cannot be black — when looking at the thick borders in this row — because otherwise a block of 1, 3 or 5 would be created.

Step 3

In row 4, there should be exactly one block of 3. The 3rd and 4th cell belong to a region. If they were free, no block of 3 would be possible in this row. That's why they have to be black.

Step 4

In column 1, there should be exactly one block of 1. The two bottom cells belong together and would form a block of 2 if they were black. Therefore, they must be marked as free.

Step 5

In column 3, there should be exactly one block of 4. There is only one possibility remaining for its position and we can draw it in completely. One cell is connected to another in the column to the left of it via a region. It is automatically colored in as well.
Note:
Whenever you have completely solved a row or column, you can strike out the number information.

Step 6

In column 4, there should only be blocks of 1. The cells above and below the existing black cell must therefore be free. Flooding also marks another cell in an adjacent column as free.

Step 7

Step 8

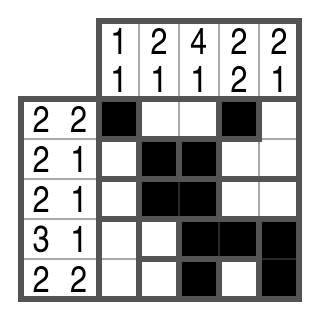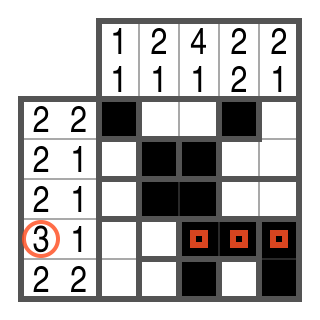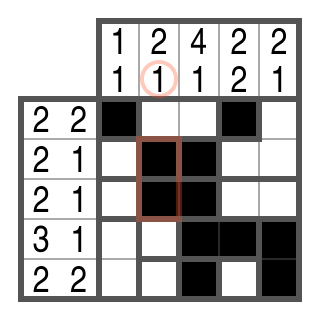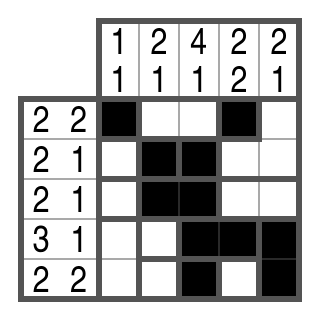
The Campixu is solved!

Even if you know the Campixu rules, every beginning is difficult. Here we show you the most important techniques to solve Campixu puzzles successfully.

Regions that must be empty (part 1)

(a)

In example (a), 3 cells should be black. A region of 4 is therefore already much too large and is marked as free.

(b)

If the region of 3 were black in example (b), the number of black cells (here: 4) would be exceeded. Therefore, the region must be marked as free.

Regions that must be empty (part 2)

(c)

If both numbers are identical as in example (c) (here: 3 and 3), this means that all blocks are blocks of 1. Regions that are larger than 1 cell must therefore be free.

(d)

If, as in example (d), the first number is 1 greater than the second number (here 4 and 3), then there are certainly no blocks that are longer than 2 cells.

Long single blocks

(e)

If exactly 1 block is required as in example (e) and this block is long enough, a slide technique can be used. In your mind, position the block as far to the left as possible and as far to the right as possible. Where the two extreme positions overlap, the cells can be colored in black. In the example we can color in 2 cells at first. In addition, we can fill in another cell at the right, because it belongs to the same region. This also means that the first cell of the row must be free, since the large block can no longer reach it.

Regions that must be black

(f)

If we didn’t color in the region of 3 in example (f), there still would be 6 available cells. But since there should be 3 blocks, the 2 spaces between the blocks must also be taken into account. Conclusion: The region of 3 is black.

(g)

If the cell at the 6th position in example (g) were marked as free, 3 blocks would result. But since there should only be 2 blocks, the cell must be black.

Further examples

(h)

In example (h), there should be exactly one block of 3. The region of 2, which extends over the 6th and 7th cells, cannot be black, since the neighboring regions are so large that a block of 4 or 5 would result.

(i)

In example (i), there should be 2 blocks. One block is already completed, the position of the second block is known. That's why we can position it exactly and finish the row.

Techniques for Color Campixu

(j)

In example (j), there should only be blocks of 1 for both colors. The region of 2 can therefore be marked as free.
In general: Regions that must be free for each color individually, can be marked as free.

(k)

In example (k), there should be a red block of 3 and a black block of 1. No matter how you place the red block of 3 in your mind (see example (e)), the middle cell must be red.
In general: A region that must be colored when looking at a single color, can actually be filled with that color.

(l)

The block of 2 in example (l) has already been placed. However, the cells to the left and right may not be marked as free, because the red block could be placed there. In this example, no step is possible.

(m)

Example (m): The black block of 1 in column 1 cannot be placed in either the first or the fourth row because no black should appear in these rows. Rows 2 and 3 can also be excluded, otherwise a block of 2 would be created. That's why only the fifth row remains.

(n)

Example (n): The cell in column 4 / row 4 cannot be black, because no black should appear in this row. It cannot be red either, because otherwise a red block of 2 would be created in column 4. Therefore, it must be marked as free.

Besides the solution techniques presented here, there are many more, of course. You will certainly find these out by yourself in the course of time. Have fun!