Nonogramme

Nonogramme sind knifflige Logik-Rätsel, die Sie am Ende mit einem Lösungsbild belohnen. Füllen Sie manche Kästchen aus und markieren Sie andere als frei — Schritt für Schritt kommen Sie dem Ziel näher.

Regeln für schwarz-weiße Nonogramme

• Jede Zahl steht für die Länge eines Kästchen-Blocks (Gruppierung schwarzer Kästchen).
• Die Reihenfolge der Zahlen entspricht genau der tatsächlichen Reihenfolge der Kästchen-Blöcke.
• Die Länge und die Abfolge der Blöcke ist also bekannt, nicht jedoch deren exakte Position.
• Zwischen zwei schwarzen Blöcken muss sich stets mindestens ein freies Kästchen befinden!

Regeln für farbige Nonogramme

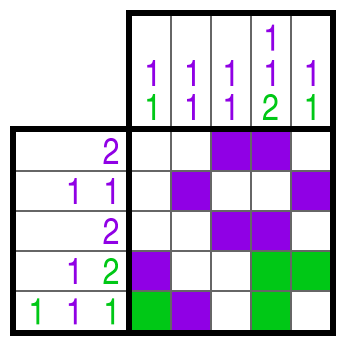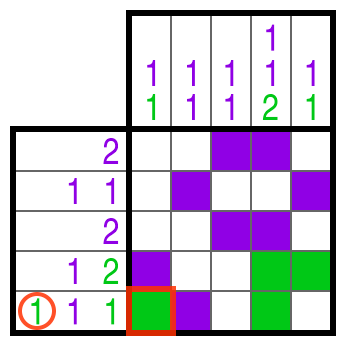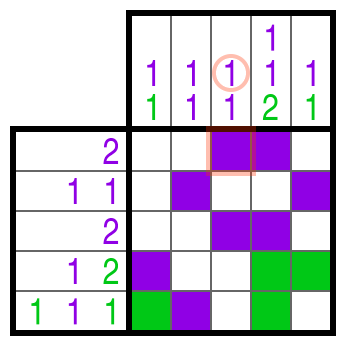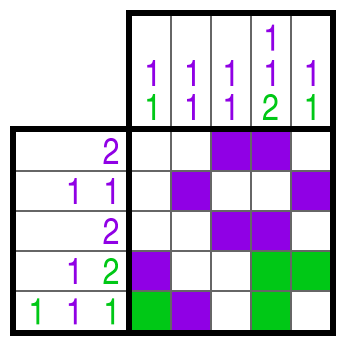
Farb-Nonogramme funktionieren im Prinzip genauso wie die schwarz-weißen Nonogramme. Zwei Dinge gibt es aber zu beachten:

• Die Farbe einer Zahleninformation gibt die Farbe des Kästchenblocks vor.
• Zwischen zwei verschiedenfarbigen Blöcken muss nicht unbedingt ein freies Kästchen sein.

Beispiel für ein schwarz-weißes Nonogramm

Im Folgenden zeigen wir Ihnen Schritt für Schritt, wie man ein kleines schwarz-weißes Nonogramm löst. Normale Nonogramme sind natürlich größer und aus ihnen ergibt sich dann ein richtiges Bild.

Schritt 1

In Zeile 2 gibt es 3 Möglichkeiten, die beiden Blöcke zu positionieren. Dabei ist das 2. Kästchen der Zeile immer schwarz. Deshalb können wir es anmalen.
Hinweis:
Wie Sie auch bei größeren Nonogrammen den Durch- und Überblick für solche Schritte behalten, erklären wir Ihnen bei "Lösungstechniken" (Stichwort Verschiebetechnik).

Schritt 2

In der 5. Zeile ist ein 3er-Block zu positionieren. Auch hierfür gibt es nur 3 Möglichkeiten. In jedem der 3 möglichen Fälle ist das dritte Kästchen der Zeile schwarz; deshalb malen wir es schwarz an.

Schritt 3

In Spalte 3 ist die genaue Position des 3er-Blocks nun klar. Wir tragen ihn vollständig ein und können die Zahleninfo "3" durchstreichen.
Weil außer diesem Block kein anderer Block in der Spalte gefordert ist, können wir die zwei verbleibenden Kästchen als frei markieren (mit einem kleinen Punkt).
Hinweis:
Generell gilt: Immer wenn Sie wissen, dass ein Kästchen frei bleiben muss, markieren Sie dieses Kästchen mit einem Punkt!

Schritt 4

Schritt 5

Schritt 6

Schritt 7

Schritt 8

Das Nonogramm ist gelöst!

Bei "Lösungstechniken" erhalten Sie tiefergehende Informationen über das Lösen von schwarz-weißen und farbigen Nonogrammen.

Auch wenn man die Nonogramm-Regeln kennt, ist aller Anfang schwer. Hier zeigen wir Ihnen die wichtigsten Techniken, um Nonogramme erfolgreich zu lösen.

Verschiebetechnik (1)

(a)

Wo der 7er-Block in Abbildung (a) genau ist, weiß man nicht, aber es gibt einige Kästchen, die auf jeden Fall schwarz sind. Wie findet man sie? Man platziert den Block in Gedanken (oder mithilfe von Abzählpfeilen, siehe unten) so weit links wie möglich und so weit rechts wie möglich. Dort, wo sich die beiden Extremfälle überschneiden, befindet sich auf jeden Fall ein Teil des Blocks, und wir können die entsprechenden Kästchen schwarz anmalen. Wenn man Nonogramme auf Papier spielt, macht man für gewöhnlich leichte Markierungen, wenn man die Kästchen von beiden Seiten abzählt. Mit dem Abzähl-Modus und den blauen Abzählpfeilen unserer App ist dies auch auf dem Bildschirm möglich!

(b)

Gibt es hingegen keine Überschneidung wie mit dem 4er-Block in Abbildung (b), können keine Kästchen eingefärbt werden.

Verschiebetechnik (2)

(c)

Die Verschiebetechnik lässt sich natürlich auch anwenden, wenn es mehr als einen Block in der betreffenden Zeile oder Spalte gibt, siehe dazu Abbildung (c). Wieder platziert man in Gedanken (oder mithilfe der Abzählpfeile) die Blöcke so weit links wie möglich. Wichtig ist, daran zu denken, dass zwischen zwei gleichfarbigen Blöcken mindestens ein Kästchen frei sein muss. Dann platziert man die Blöcke so weit rechts wie möglich. Dort, wo es Überschneidungen desselben Blocks gibt, können die Kästchen angemalt werden.

Verschiebetechnik (3)

(d)

Wenn wie in Abbildung (d) schon Kästchen bestimmt sind, können diese bei der gedanklichen Verschiebung mit berücksichtigt werden, um evtl. noch mehr Überschneidung zu erreichen. In unserem Beispiel bedeutet dies konkret: Der 2er-Block kann wegen des bereits als frei markierten Kästchens nicht weiter links platziert werden. Bei der Gegenrichtung kann der 4er-Block nicht weiter rechts als gezeigt positioniert werden. Dadurch ergibt sich mehr Überschneidung als im vorherigen Beispiel.

Verschiebetechnik (4)

(e)

Da bei farbigen Nonogrammen zwischen zwei verschiedenfarbigen Blöcken nicht unbedingt ein freies Kästchen sein muss, reihen sich die Abzählpfeile, die zu unterschiedlichen Farben gehören, generell ohne Zwischenraum aneinander (dies wird im Beispiel (e) beim Zählen von links nach rechts gezeigt).
Bei farbigen Nonogrammen kann jedoch noch zusätzlich Information gewonnen werden: Betrachtet man eine Zeile, können die Zahleninfos aus den Spalten (und auch die bereits in den Spalten eingetragenen Kästchen) wichtige Informationen liefern. (Analog dazu kann man bei der Betrachtung einer Spalte auch Informationen aus den Zeilen gewinnen.)
In unserem konkreten Beispiel soll es in der 6. Spalte nur einen schwarzen 7er-Block geben. Das sagt uns, dass der rote 4er-Block der betrachteten Zeile nicht die 6. Spalte treffen kann. Die Extrempositionierung des 4er-Blocks liegt somit drei Kästchen weiter links als ohne diese Zusatzinformation.

Weitere Beispiele

Beispiel (f)

(f)

Beispiel (g)

(g)

Beispiel (h)

(h)

Beispiel (i)

(i)

Beispiel (j)

(j)

Techniken bei farbigen Nonogrammen

In Abbildung (e) wurde bereits auf die farbigen Nonogramme eingegangen. Hier folgen drei weitere Beispiele, die speziell Situationen bei farbigen Nonogrammen zeigen.

(k)

In der ersten Zeile soll ein schwarzer 1er-Block platziert werden. Da in den Spalten 4 und 5 nur rote Blöcke vorgesehen sind, müssen die Schnittpunkte frei sein. In Spalte 2 gibt es zwar einen schwarzen 2er-Block, aber über ihm soll es einen roten 1er-Block geben. Deswegen muss das Kästchen in Zeile 1 / Spalte 2 frei sein.

(l)

In allen Zeilen – mit Ausnahme von Zeile 2 – ist zuerst ein schwarzer Block vorgesehen. Deswegen kann der rote 1er-Block von Spalte 1 nur in Zeile 2 platziert werden.

(m)

In Spalte 3 ist der rote Block schon platziert. Das heißt, dort fehlt nur noch der schwarze Block. Deshalb kann das dritte Kästchen von Zeile 2 nicht rot sein und muss deswegen frei sein.

Neben den hier vorgestellten Lösungstechniken gibt es natürlich noch viele weitere. Diese werden Sie sicherlich im Laufe der Zeit selbst herausfinden. Viel Spaß dabei!