Campixu
Campixu ist ein kniffliges Logik-Rätsel, das Sie am Ende mit einem Lösungsbild belohnt. Füllen Sie manche dick umrandeten Regionen aus und markieren Sie andere als frei — Schritt für Schritt kommen Sie dem Ziel näher.
Campixu wurde 2008 von Johannes Kestler erfunden und erschien erstmals in der Zeitschrift LOGIC PIXELS im August 2008. Inzwischen sind diese Rätsel auch unter den Namen „Cross-a-Pix“ und „PoliPix“ bekannt. Auf den ersten Blick schaut Campixu wie Nonogramme aus, und es bestehen tatsächlich Ähnlichkeiten mit den Nonogrammen. Aber da die Regeln unterschiedlich sind, sind die Lösungsstrategien, also die Techniken, mit denen man einem Campixu das Lösungsbild entlockt, komplett anders, sodass Campixu ein total neues Rätselerlebnis darstellt.
Wer Nonogramme mag, liebt Campixu!
Im Dezember 2017 erfand Johannes Kestler die Farb-Variante von Campixu. Farb-Campixus wurden der Öffentlichkeit zum ersten Mal im März 2019 mit der App Let’s IQ Campixu vorgestellt.
Regeln für schwarz-weißes Campixu
Zahlen
- Jede Zeile und Spalte besitzt genau zwei Zahlen.
- Die erste Zahl gibt an, wie viele Kästchen in der betreffenden Zeile bzw. Spalte schwarz sind (unabhängig von ihrer Gruppierung).
- Die zweite Zahl gibt an, wie viele schwarze Blöcke (Gruppen) sich in der betreffenden Zeile bzw. Spalte befinden. Dabei ist ein Block eine Aneinanderreihung von schwarzen Kästchen (der Mindestlänge 1). Zwischen zwei Blöcken muss mindestens ein Kästchen frei sein, um sie zu trennen.
- [5 3] liest sich also: „5 Kästchen sind in 3 Blöcken untergebracht.“ Das kann 1+1+3 oder 1+3+1 oder 3+1+1 oder 1+2+2 oder 2+1+2 oder 2+2+1 bedeuten. Die genaue Position und Reihenfolge der Blöcke ist nicht vorgegeben.
Dick umrandete Regionen
- Die Kästchen in dick umrandeten Regionen haben alle dieselbe Farbe. Entweder sind alle Kästchen in einer Region schwarz oder alle Kästchen sind frei.
- Hat man also ein Kästchen eindeutig bestimmt, kann man die übrigen Kästchen der dick umrandeten Region genauso markieren (Region fluten).
Regeln für Farb-Campixu
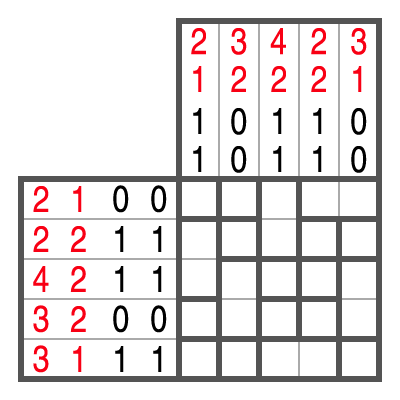
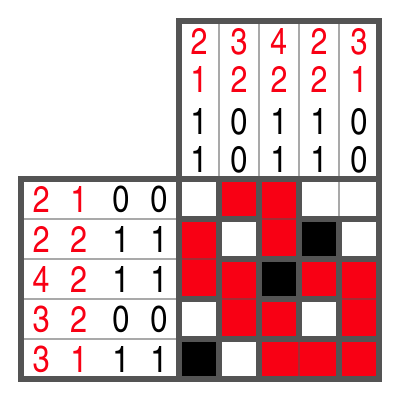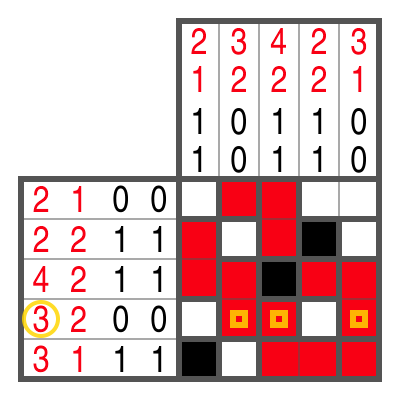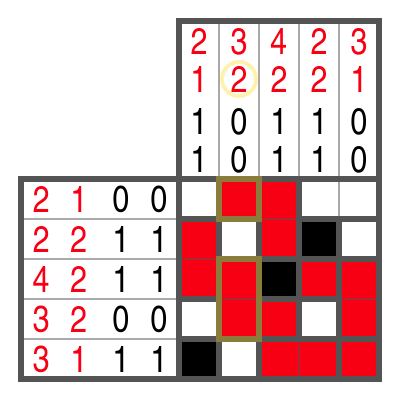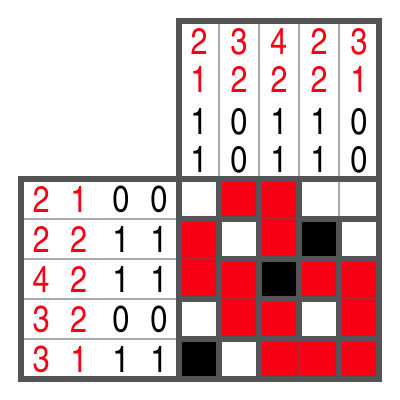
Farb-Campixu funktioniert im Prinzip genauso wie die schwarz-weiße Variante. Drei Dinge gibt es aber zu beachten:
- Für jede Farbe gibt es zwei Zahleninfos in jeder Zeile und Spalte, die angeben, wie viele Kästchen bzw. Blöcke der jeweiligen Farbe vorhanden sind.
- Zwischen zwei verschiedenfarbigen Blöcken muss nicht unbedingt ein freies Kästchen sein.
- Die Reihenfolge der Farben ist nie vorgegeben.
Beispiel
Beispiel für ein schwarz-weißes Campixu
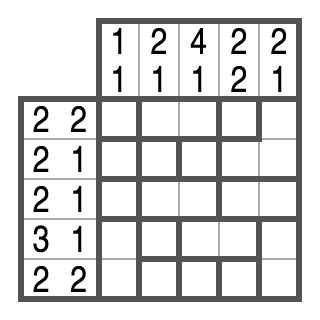
Im Folgenden zeigen wir Ihnen Schritt für Schritt, wie man ein kleines schwarz-weißes Campixu löst. Normale Campixu-Rätsel sind natürlich größer.
Schritt 1
In Zeile 1 sollen 2 Kästchen in 2 Blöcken untergebracht werden. Das heißt, dass jeder Block genau 1 Kästchen breit sein soll. Weil das 2. und das 3. Kästchen zur selben Region gehören, würden sie einen 2er-Block bilden, wenn man sie schwarz färben würde. Deshalb müssen sie als frei markiert werden.
Hinweis:
Generell gilt: Immer wenn Sie wissen, dass Kästchen frei bleiben müssen, markieren Sie diese Kästchen mit einem Punkt!
Schritt 2
In Zeile 3 soll es genau einen 2er-Block geben. Das erste Kästchen kann — bei Betrachtung der dicken Linienbegrenzungen in dieser Zeile — nicht schwarz sein, weil sonst ein 1er-, 3er- oder 5er-Block entstehen würde.
Schritt 3
In Zeile 4 soll es genau einen 3er-Block geben. Das 3. und 4. Kästchen gehören zu einer Region. Wenn sie frei wären, wäre kein 3er-Block in dieser Zeile möglich. Deshalb müssen sie schwarz sein.
Schritt 4
In Spalte 1 soll es genau einen 1er-Block geben. Die zwei untersten Kästchen gehören zusammen und würden einen 2er-Block bilden, wenn sie schwarz wären. Deshalb müssen sie als frei markiert werden.
Schritt 5
In Spalte 3 soll es genau einen 4er-Block geben. Für dessen Position gibt es nur noch eine Möglichkeit und wir können ihn vollständig einzeichnen. Ein Kästchen ist über eine Region mit einem anderen in der Spalte links daneben verbunden. Es wird automatisch mit eingefärbt.
Hinweis:
Immer wenn Sie eine Zeile oder Spalte vollständig gelöst haben, können Sie die Zahleninfos ausstreichen.
Schritt 6
In Spalte 4 soll es nur 1er-Blöcke geben. Über und unter dem bereits existierenden schwarzen Kästchen müssen die Kästchen deshalb frei sein. Durch das Fluten wird auch ein anderes Kästchen in einer benachbarten Spalte als frei markiert.
Schritt 7
Schritt 8
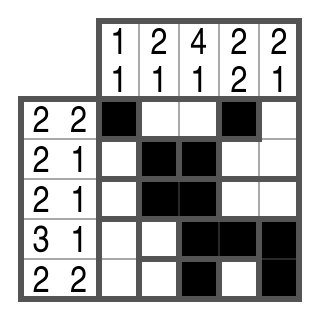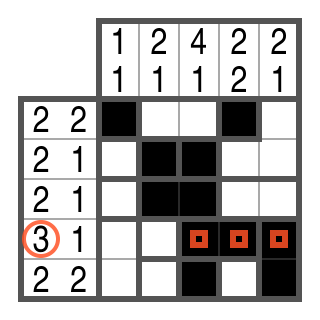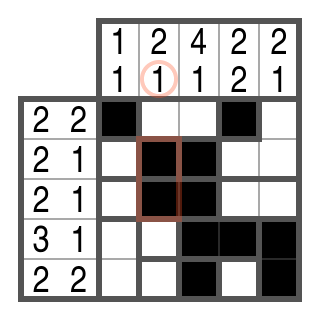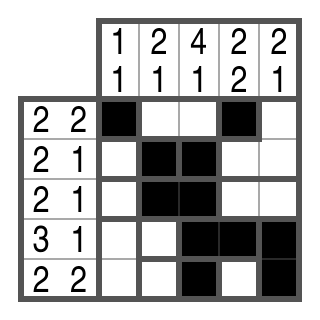
Das Campixu ist gelöst!
Lösungstechniken
Auch wenn man die Campixu-Regeln kennt, ist aller Anfang schwer. Hier zeigen wir Ihnen die wichtigsten Techniken, um Campixu-Rätsel erfolgreich zu lösen.
Regionen, die leer sein müssen (Teil 1)
(a)
In Beispiel (a) sollen 3 Kästchen schwarz sein. Eine 4er-Region ist deshalb schon grundsätzlich viel zu groß und wird als frei markiert.
(b)
Wenn die 3er-Region in Beispiel (b) schwarz wäre, wäre die schwarze Kästchenanzahl von 4 überschritten. Deshalb muss die Region als frei markiert werden.
Regionen, die leer sein müssen (Teil 2)
(c)
Wenn beide Zahlen wie in Beispiel (c) identisch sind (hier: 3 und 3), bedeutet dies, dass alle Blöcke 1er-Blöcke sind. Regionen, die größer als 1 Kästchen sind, müssen demnach frei sein.
(d)
Wenn wie in Beispiel (d) die erste Zahl um 1 größer als die zweite Zahl ist (hier 4 und 3), dann gibt es sicher keine Blöcke, die länger als 2 Kästchen sind.
Lange einzelne Blöcke
(e)
Wenn genau 1 Block wie in Beispiel (e) gefordert ist und dieser Block lang genug ist, kann man eine Verschiebetechnik anwenden. Man positioniert den Block in Gedanken so weit links wie möglich und so weit rechts wie möglich. Dort, wo sich beide Extrem-Platzierungen überschneiden, kann man die Kästchen schwarz anmalen. Im Beispiel können wir also zunächst 2 Kästchen anmalen. Zusätzlich können wir ein weiteres Kästchen rechts schwärzen, weil es zur selben Region gehört. Damit ist dann auch verbunden, dass das erste Kästchen der Zeile frei sein muss, da der große Block es nicht mehr erreichen kann.
Regionen, die schwarz sein müssen
(f)
Wenn wir die 3er-Region in Beispiel (f) nicht schwarz ausmalen würden, gäbe es zwar noch 6 verfügbare Kästchen. Aber da es 3 Blöcke sein sollen, müssen auch die zwei Zwischenräume zwischen den Blöcken mit berücksichtigt werden. Fazit: Die 3er-Region ist schwarz.
(g)
Wenn das Kästchen an 6. Stelle in Beispiel (g) als frei markiert wäre, würden sich 3 Blöcke ergeben. Da es aber nur 2 Blöcke geben soll, muss das Kästchen schwarz sein.
Weitere Beispiele
(h)
In Beispiel (h) soll es genau einen 3er-Block geben. Die 2er-Region, die sich über das 6. und 7. Kästchen erstreckt, kann nicht schwarz sein, da die Nachbar-Regionen so groß sind, dass sich ein 4er- oder 5er-Block ergeben würde.
(i)
In Beispiel (i) soll es 2 Blöcke geben. Ein Block ist schon abgeschlossen, vom zweiten Block ist die Position bekannt. Deshalb können wir auch ihn genau positionieren und die Zeile abschließen.
Techniken für Farb-Campixu
(j)
In Beispiel (j) soll es für beide Farben nur 1er-Blöcke geben.
Die 2er-Region kann also als frei markiert werden.
Generell gilt: Regionen, die für jede Farbe betrachtet frei sein müssen, können als frei markiert werden.
(k)
In Beispiel (k) soll es einen roten 3er-Block und einen schwarzen 1er-Block geben.
Egal, wie man den roten 3er-Block gedanklich platziert (siehe Beispiel (e)), das mittlere Kästchen muss rot sein.
Generell gilt: Eine Region, die bei Betrachtung einer einzelnen Farbe farbig sein muss, kann tatsächlich mit dieser Farbe gefüllt werden.
(l)
Der 2er-Block in Beispiel (l) ist bereits eingetragen. Man darf aber die Kästchen links und rechts davon nicht als frei markieren, weil der rote Block dort platziert werden könnte. In diesem Fall ist also kein Schritt möglich.
(m)
Beispiel (m): Der schwarze 1er-Block in Spalte 1 kann weder in der 1. noch in der 4. Zeile platziert werden, weil in diesen Zeilen kein Schwarz vorkommen soll. Zeilen 2 und 3 sind auch ausgeschlossen, weil sonst ein 2er-Block entstehen würde. Deswegen bleibt nur die 5. Zeile übrig.
(n)
Beispiel (n): Das Kästchen in Spalte 4 / Zeile 4 kann nicht schwarz sein, weil in dieser Zeile kein Schwarz vorkommen soll. Es kann auch nicht rot sein, weil sonst in Spalte 4 ein roter 2er-Block entstehen würde. Deswegen muss es als frei markiert werden.
Neben den hier vorgestellten Lösungstechniken gibt es natürlich noch viele weitere. Diese werden Sie sicherlich im Laufe der Zeit selbst herausfinden. Viel Spaß dabei!
